この記事はCompetitive Programming Advent Calendar 2017の9日目の記事です。
セグメントツリーにセグメントツリーを乗せる?と何が出来るのか
- 端的に言うと2Dセグメントツリーが構成できる
- 一部の2Dセグメントツリーをよりメモリ効率良く作れるというだけ
- 以下の説明はセグメントツリーがまず分かっていないと理解するのは厳しい
- 下に画像があるが、見にくい場合にはslideshareにも上げてあるので、そちらを見て欲しい これ
使わないほうがいい問題
これらの問題ではなるべく普通の2Dセグメントツリーを使った方がいい。
理由は
- H*Wの配列に全て数が書かれている
- しかもメモリ上にO(HW)が乗る
からである。本手法は全てに数が書かれている場合は普通の2Dセグメントツリーよりもメモリ効率が悪くなるので、最悪MLEする。
使える問題
これらの問題の解法の中で2Dセグメントツリーが出て来るが、以下のような性質がある。
「H*Wの配列に数を入れていくが、HもWも最大10^5くらい」
普通の2Dセグメントツリーで管理するとO(HW)のメモリとなるので、これはメモリ上に乗らない。
例題
使える問題で紹介した問題ではちょっとした考察や他のアルゴリズムを必要とするので、わかりやすく以下の問題で説明しよう。
H*Wの行列Aがあり、全ての値は0になっている。 Q個のクエリを順番に処理せよ。 クエリ1: "1 x y v": A[y][x]にvを追加する クエリ2: "2 sx sy tx ty": 左上(sx,sy)で右下(tx,ty)の長方形の領域の数の総和を答えよ なお、全て0-indexedで与えられる。 入力 1行目が"H W Q" 2~Q+1行目がクエリ 1≦H,W≦10^5 1≦Q≦10^5 0≦v≦10^9 x,y,sx,sy,tx,tyは正しく与えられる Sample 入力 8 8 5 1 2 4 1 1 5 3 6 1 3 3 2 2 0 0 4 4 2 2 2 5 5 出力 3 9
愚直にセグメントツリーにセグメントツリーを乗せてみる
普通に2Dセグメントツリーを作るとO(HW)でダメになる。
そこで、「セグメントツリーにセグメントツリーを乗せて」みよう。
上のサンプルで考えてみる。
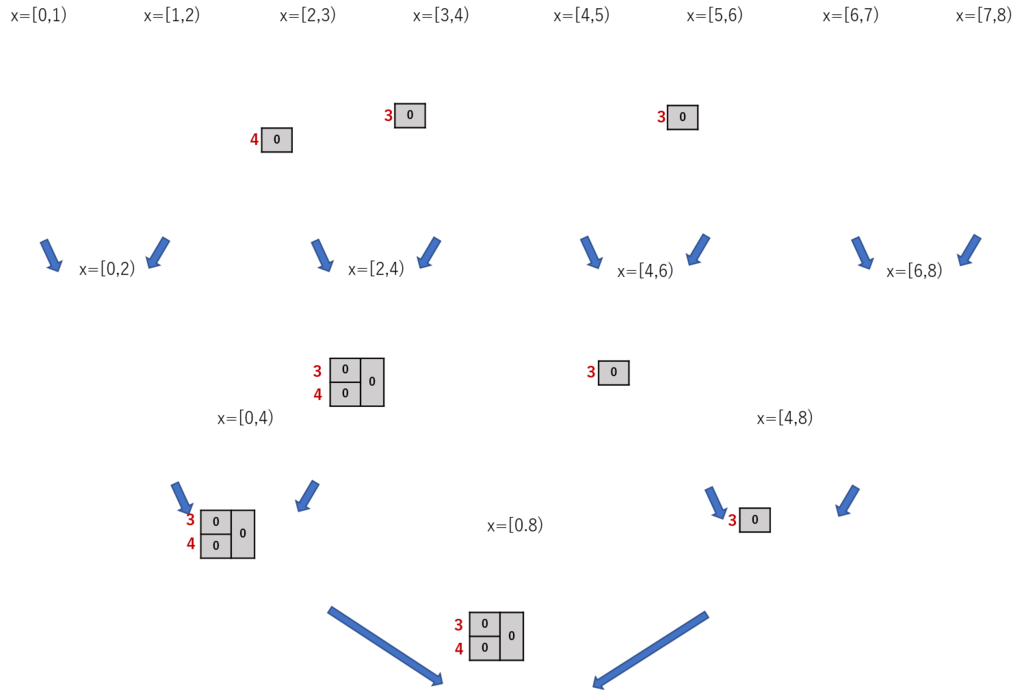
まず、以下のように初期化する。
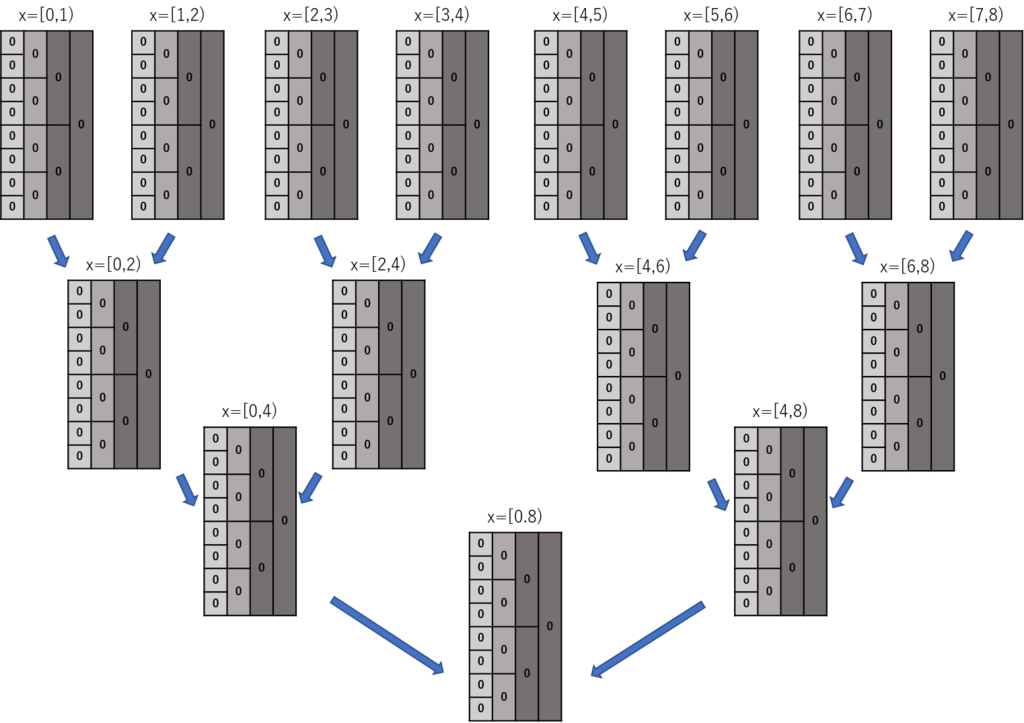
これで最初のクエリを処理してみよう。
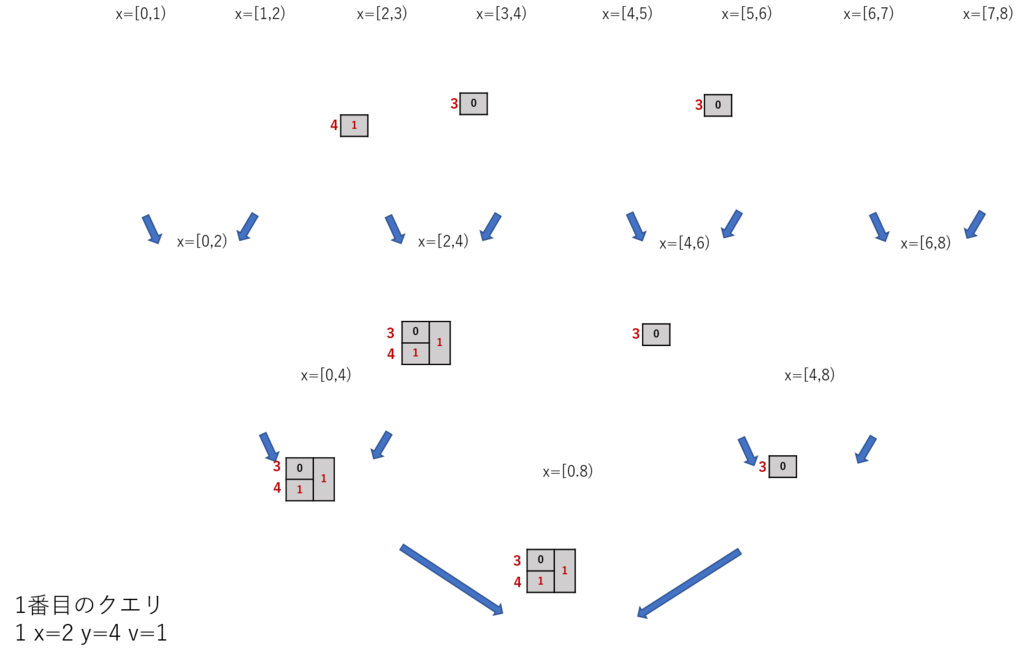
「1(add) x=2 y=4 v=1」
x=[2,3)のセグメントツリーのy=4に1を追加する
次に、親にそれを伝搬させていく。
x=[2,4)とx=[0,4)とx=[0,8)でも同様に更新する
更新作業はO(logWlogH)だけかかる
結果はこうなる
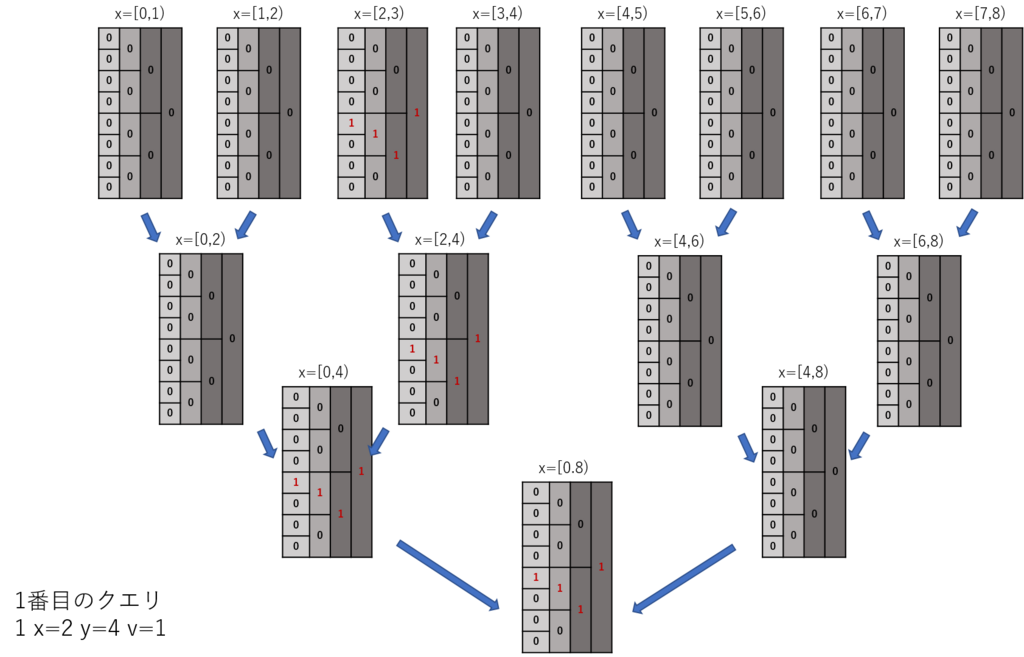
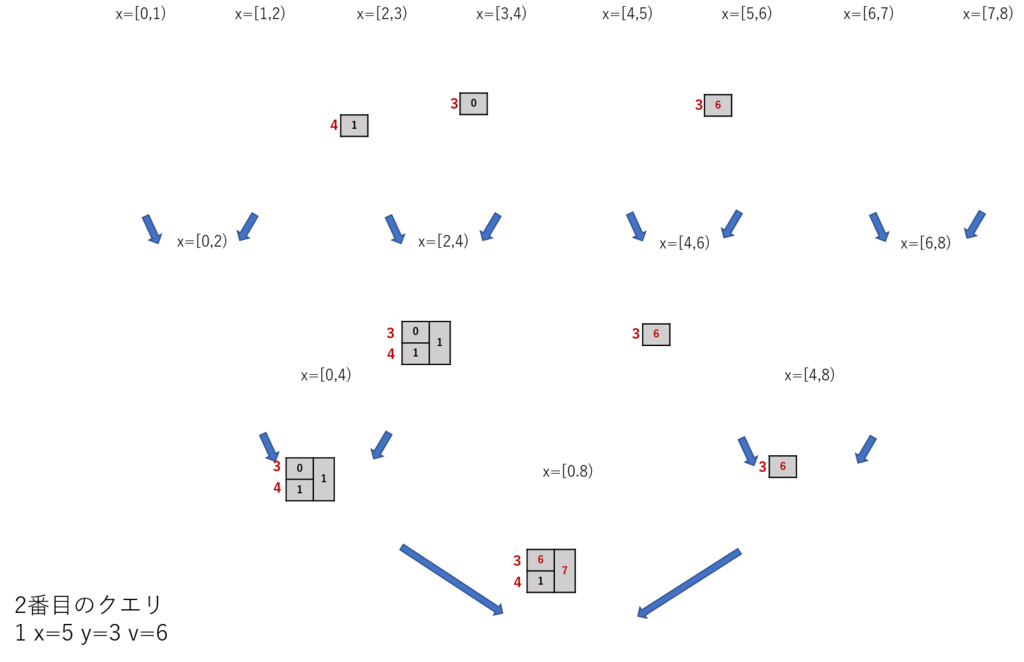
2番目のクエリも同様に処理するとこうなる。
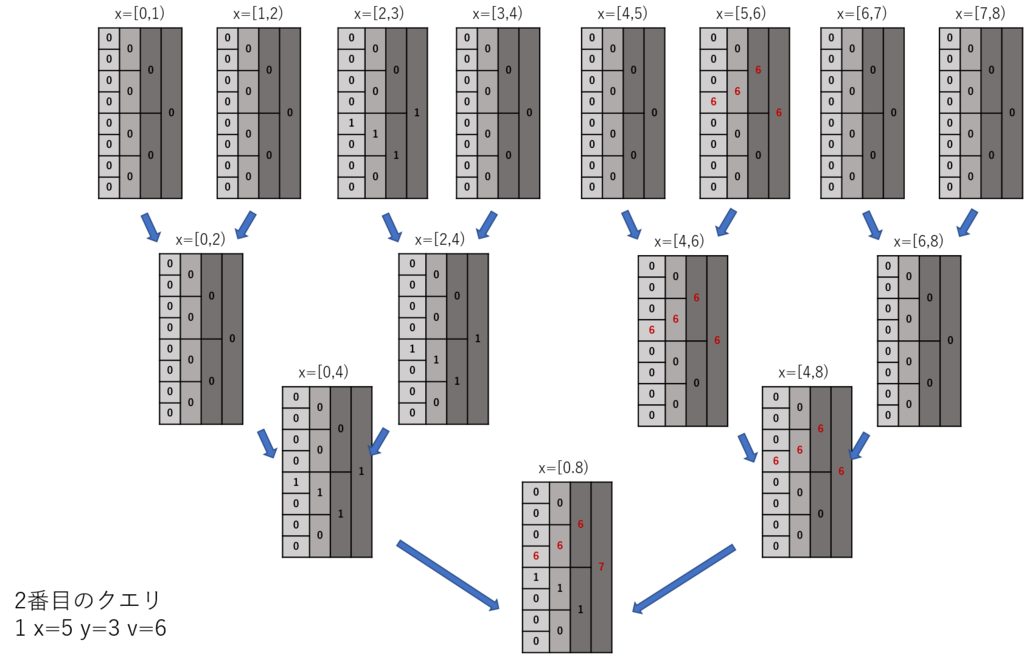
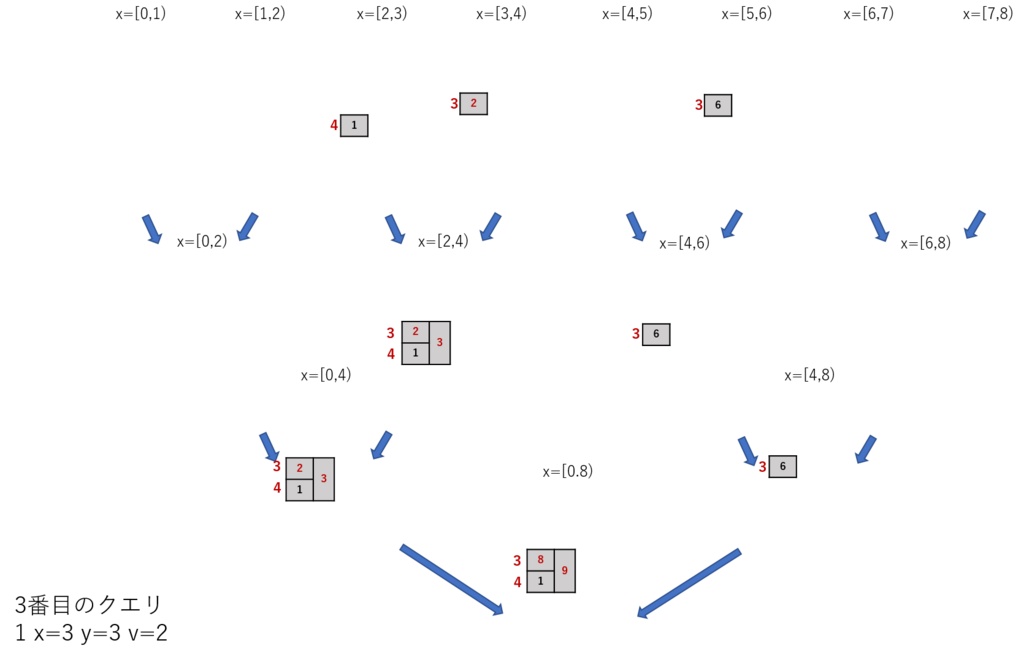
3番目のクエリをやるとこう。
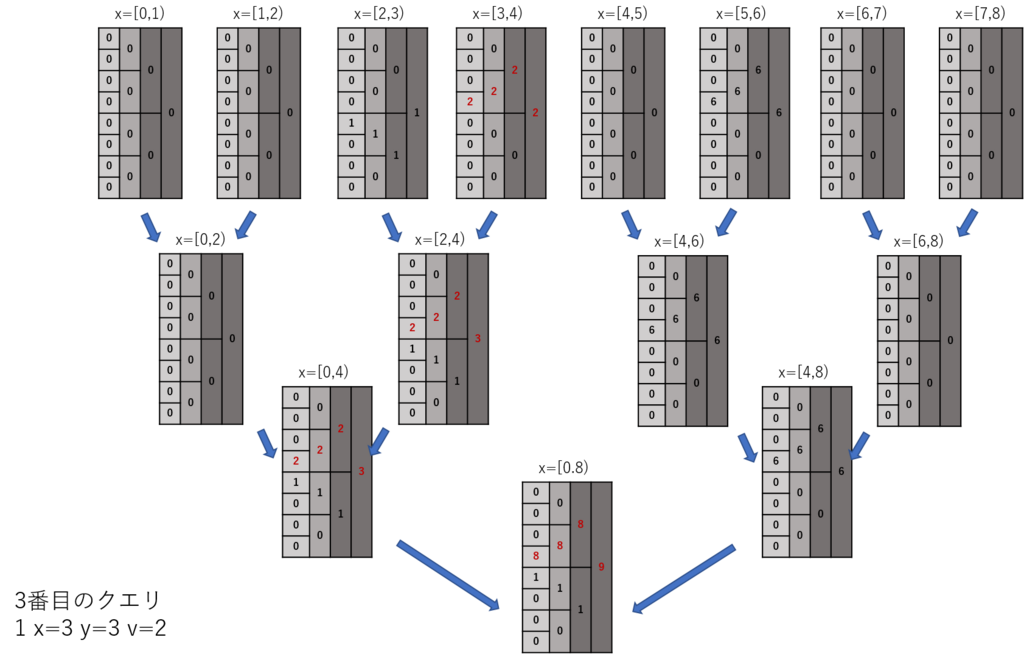
さて、次はクエリ2の方だが、セグメントツリーで取ってくる感じでセグメントツリーをx座標で限定して取ってくる。
そして、取ってきたセグメントツリーは高々O(logW)個で、それぞれのセグメントツリーからy座標で限定して取ってきてマージする。
取得作業もO(logWlogH)だけかかる。
これで全部合計すると"3"
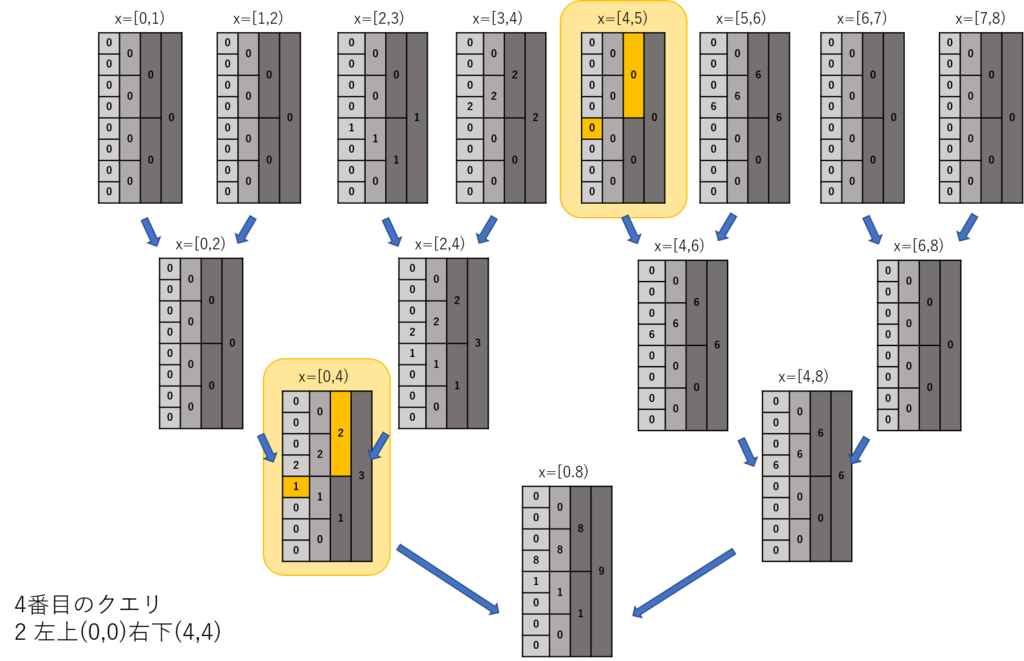
最後のクエリも同様にやってみるとこうなる
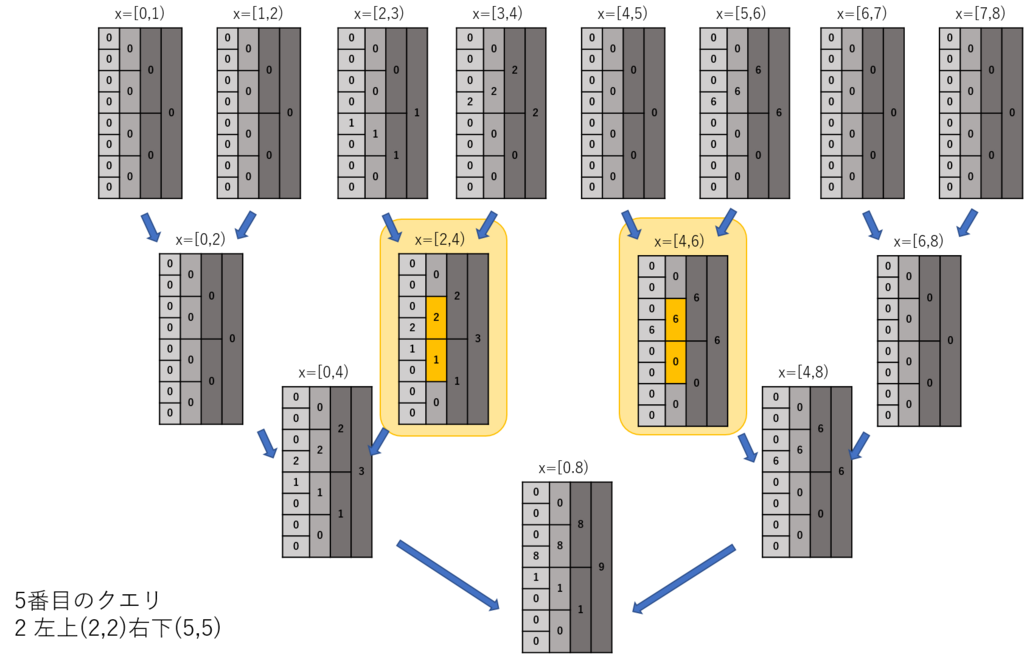
以上に示したのは普通の2Dセグメントツリーである。
つまり、「セグメントツリーにセグメントツリーを乗せる」ととりあえず時間計算量は問題ない。
あとは、空間計算量である。このやり方だとO(HW)のメモリを食うので、今回の例題を解くことは出来ない。
セグメントツリーにセグメントツリーを乗せる手法
H,Wが10^5となる場合では全ての要素が更新される事はありえない。
(クエリの総数が10^10とかになってしまう)
そのため、全てのセグメントツリーを作っても大部分は無駄になってしまう。
この無駄を無くしたのが、「セグメントツリーにセグメントツリーを乗せる手法」である。
さっきの例で使われた部分を見てみよう
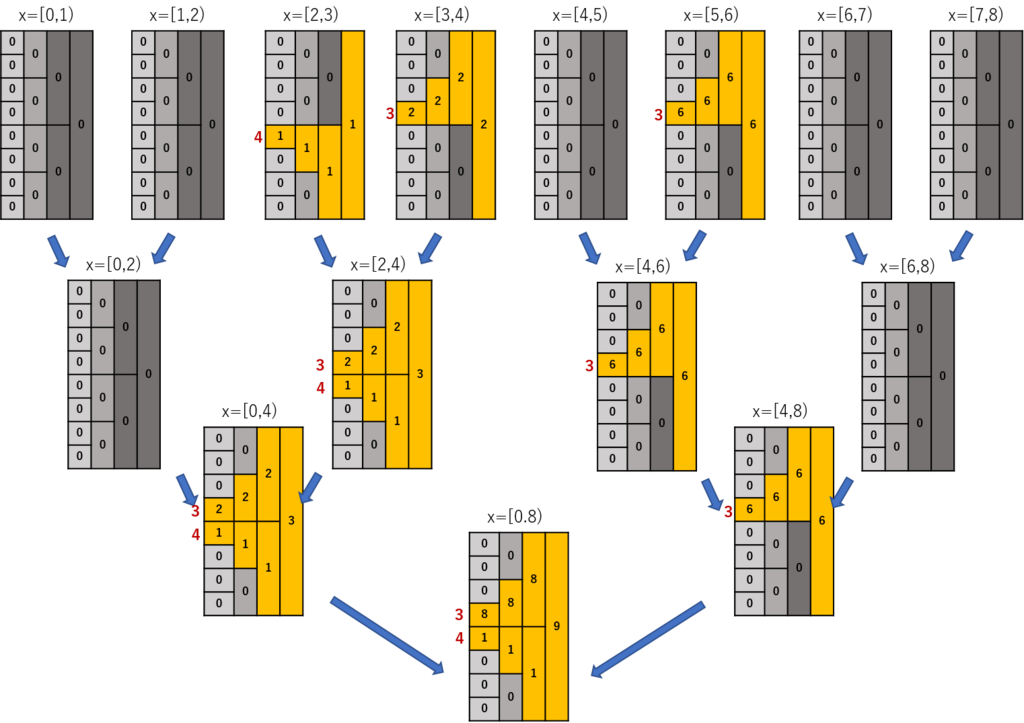
それ以外の部分はいらないので消そう。
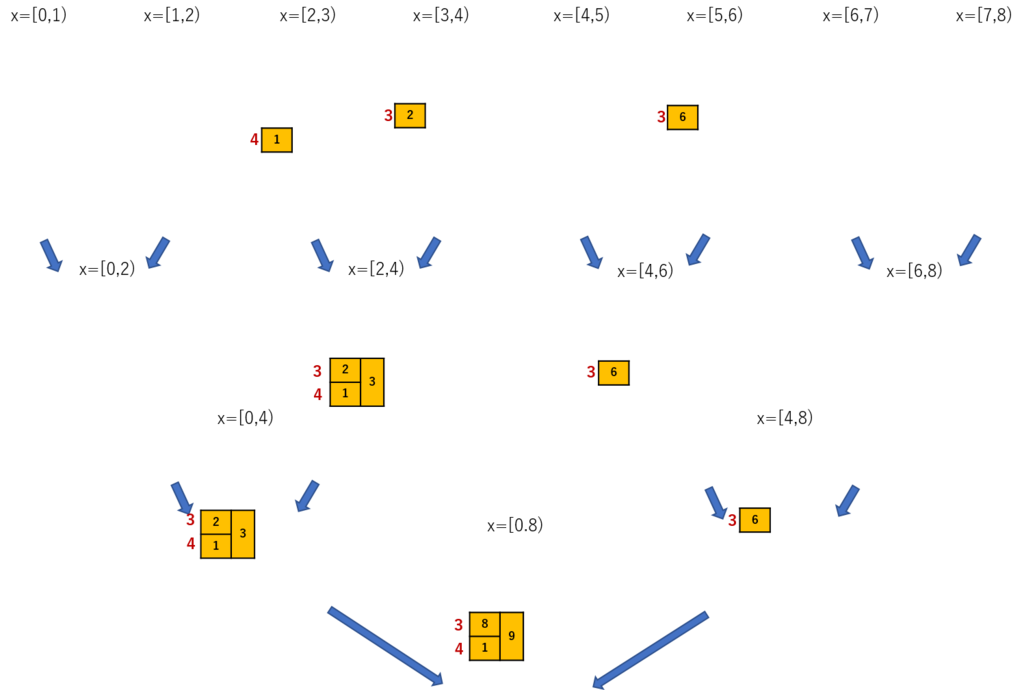
実際使われている部分はこんなに少ない。
クエリを先読みして、使われているy座標をx座標側のセグメントツリーの要素毎にまとめて、それで座標圧縮してセグメントツリーを作る。
圧縮済みのセグメントツリーでサンプルのクエリをやってみよう。
以下のように処理が進む
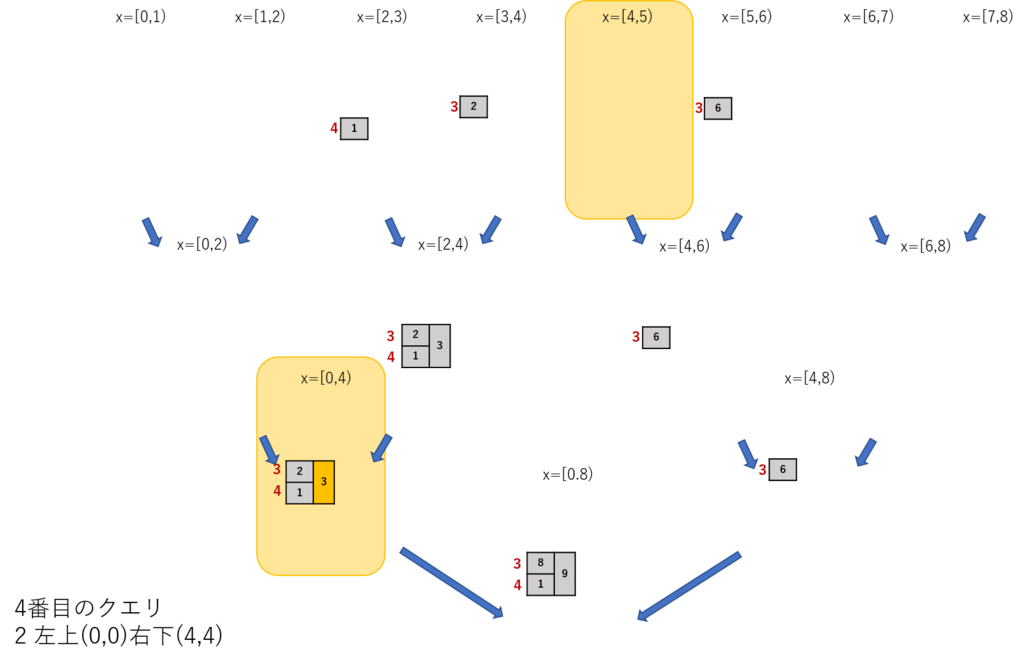
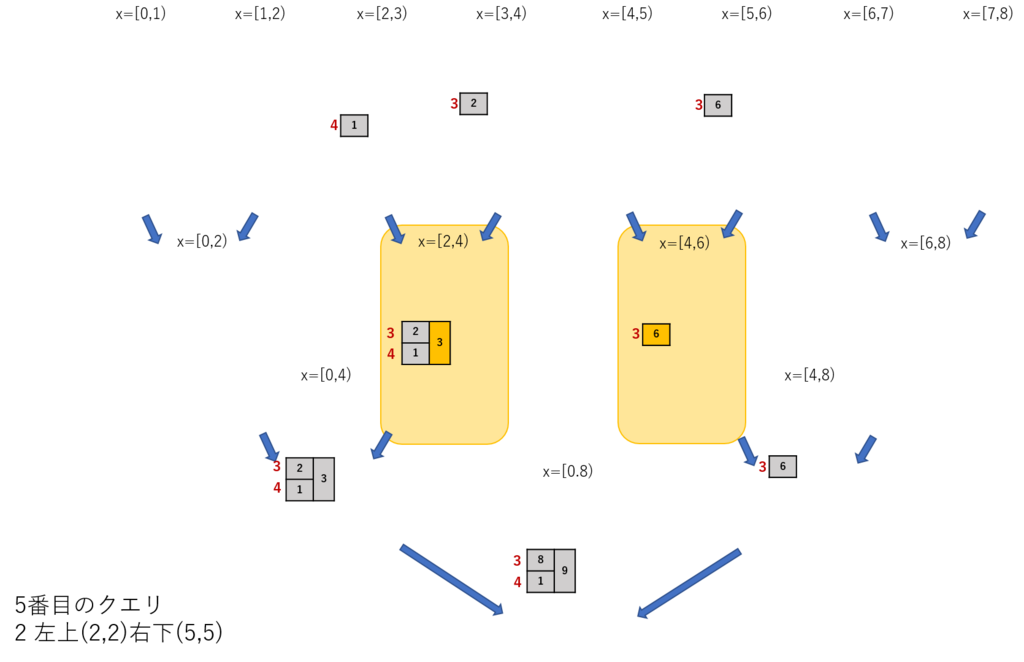
正直、空間計算量のオーダーがどのくらいでおさまるか分からないのだけど、むっちゃ削減できてMLEを回避できる。