LIS on Tree [AtCoder Beginner Contest 165 F]

https://atcoder.jp/contests/abc165/tasks/abc165_f

前提知識

• 座標圧縮
• セグメントツリーを使ったLIS解法
• 永続セグメントツリー（部分永続でOK）

解説

https://atcoder.jp/contests/abc165/submissions/12637772

データ構造ズルをして解いた。
自分は手元に完全永続セグメントツリーがあったので、それを貼った。
部分永続セグメントツリーならセグメントツリーからちょっと工夫すれば書けるので、それが想定解ではないかなと思っている。
さて、ABCにratedで出ている方には『永続データ構造』は分からない人が大半だろうと思う。
それで問題無いように解説は書いていこう。

早速だが、「座標圧縮」と「セグメントツリーを使ったLIS解法」を知らない場合は、先にそっちを学習してきてほしい。
自分と想定解が同じなら、公式解説動画でも教えてくれるかもしれないし、そっちで学んでもいい。
座標圧縮 - Google 検索
lis セグメントツリー - Google 検索
これを説明するにはちょっと長い。

さて、LISの典型として、大小関係だけが重要であるので、配列aは座圧をして、[0,N)の範囲に数を収めておこう。
頂点1から頂点kまでの最短パスを考えているが、頂点1を根とすれば、根から頂点kまでの数列のLISを求める問題になる。
ここでLISを求めるのにセグメントツリーを使ってみよう。
区間max, 1点更新ができるセグメントツリーがあれば、LISを解くことができる。
試しに分岐が無い木で考えてみると、これは通常のLISと同様であり、根から順に値を見ながら、セグメントツリーを更新していけば解ける。

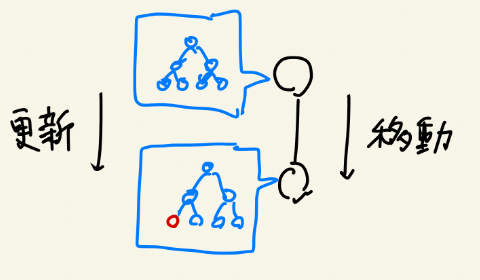
分岐があった場合は、どうなるだろうか。
木なのでDFSで頂点を見ていくが、一旦片方の更新までいって、戻ってくることになる。

この時に戻ってきたところまでセグメントツリーを「戻して」おきたくなる。
このように、ある更新地点まで戻せるデータ構造を永続データ構造という。

この戻せるセグメントツリーをいかに実装するかというのが問題だが、自分はライブラリになってるので貼ってしまった。
戻す方法の常套テクとして、履歴を残しておくという方法がある。
セグメントツリーの一点更新時に、更新場所と元々あった数をstackとかで覚えておいて、1手戻したくなったら、stackから最新の履歴を1つ取り出して適用すれば戻せる。
こういうundo機構を工夫して作ればACが得られる。
（ただ、自分のライブラリはそういうタイプじゃないので、自分の実装は参考にしないでください）

int N, a[201010];
vector<int> E[201010];
//---------------------------------------------------------------------------------------------------
PersistentSegmentTree pst;
int ans[201010];
void dfs(int cu = 0, int pa = -1, int root = 0) {
    int root2 = root;
    int ma = pst.get(root, 0, a[cu]);
    pst.update(root2, a[cu], max(pst.get(root, a[cu], a[cu] + 1), ma + 1));

    ans[cu] = pst.get(root2, 0, N);
    fore(to, E[cu]) if (to != pa) dfs(to, cu, root2);
}
//---------------------------------------------------------------------------------------------------
void _main() {
    cin >> N;
    rep(i, 0, N) cin >> a[i];
    compress1(a, N);

    rep(i, 0, N - 1) {
        int u, v; cin >> u >> v;
        u--; v--;
        E[u].push_back(v);
        E[v].push_back(u);
    }

    pst.init(N);
    dfs();

    rep(i, 0, N) printf("%d\n", ans[i]);
}