https://atcoder.jp/contests/agc043/tasks/agc043_b
解説
https://atcoder.jp/contests/agc043/submissions/11065208
まず、答えは0,1,2の3択になる。
このどれが答えになるかを求めていこう。
これは実験すると分かるし、操作を見てみるとそうなりそうなこともわかる。
次の一手を生み出すのがきつい。
答えの偶奇をまずは特定しよう。
答えの偶奇を見たいので、Aも偶奇だけを見てやればよさそう。
つまり、すべての差の計算をmod 2で計算した場合を考える。
mod 2での計算結果なので、最初のAもmod 2をして、0/1で考えて問題ない。
mod 2上では、x+yもx-yもx xor yもすべて同じ結果になる。
試してみればわかる。
よって、操作はx+yとしているのと同じ状況になる。
この問題は典型問題であり、パスカルの三角形を使って高速に計算ができる。
N要素ある時、操作後の最終的な値は C(N-1,i)*A[i]の総和 となる(i=0,1,...,N-1)。
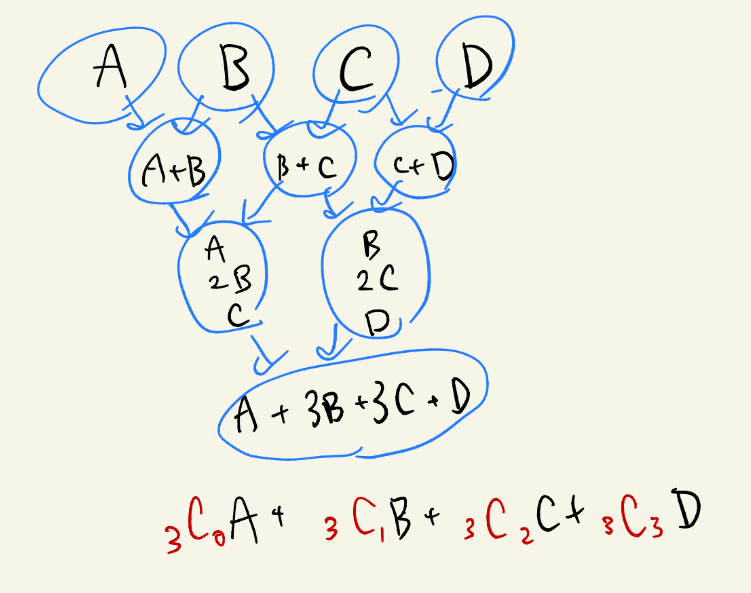
よって、C(N-1,i)の偶奇が分かれば、最終的な値の偶奇もわかる。
これはインターネットで「二項係数 偶奇」で調べると、
二項係数の偶奇(解決編) - 球面倶楽部 零八式 mark II
こんな良いサイトが出てくる。
C(n,r)%2==1 <=> n == ( r | (n - r) ) がtrue
ということらしいので、これが成り立つならば、A[i]が足される。
mod 2なので、操作はxyであると考えて、総和の代わりにxor和を使って、
二項係数が奇数であればxor 1をしている。
これで最終的に1であれば、答えは奇数なので1を答える。
次に、0か2かの判定であるが、1が含まれるのであれば答えは0となる。
これは実験をしてみると何となく分かる。
実験からエスパーしよう。
そうでないなら、Aは0と2から構成される。
0と2の操作を見てみると、0と0は0, 0と2は2, 2と0は2, 2と2は2であるため、xor操作になっている。
なので、さっきと同様にC(N-1,i)の偶奇を使って、最終的な値の偶奇を計算して、答える。
int N, A[1010101]; //--------------------------------------------------------------------------------------------------- int solve() { rep(i, 0, N - 1) A[i] = abs(A[i] - A[i + 1]); N--; int tot = 0; rep(i, 0, N) if (A[i] == 1 && (i | (N - 1 - i)) == N - 1) tot ^= 1; if (tot) return 1; rep(i, 0, N) if (A[i] == 1) return 0; tot = 0; rep(i, 0, N) if (A[i] == 2 && (i | (N - 1 - i)) == N - 1) tot ^= 2; return tot; } //--------------------------------------------------------------------------------------------------- void _main() { cin >> N; string S; cin >> S; rep(i, 0, N) A[i] = S[i] - '0'; cout << solve() << endl; }