Tree Separator [JAG Practice Contest for ACM-ICPC Asia Regional 2017 E]

https://jag2017autumn.contest.atcoder.jp/tasks/jag2017autumn_e

N頂点の木がある。
ここから1つのパスを指定して、パスに含まれる頂点と辺を全て取り除く。
できる連結成分の中で良い成分（頂点数がK以上）の個数を最大化せよ。

解法

木DPをする。
頂点1をルートとした木を考える。
　
まずdfsをしてcnt配列を作っておこう（pre関数）
cnt[cu] := 頂点cuの部分木の頂点数
　
dp[cu] := 頂点cuから親へパスの端点が伸びているときに、頂点cuの部分木で作れる良い成分の最大個数
これを作りながら答えを更新していく。
頂点cuに対してできるのは以下の4パターンである。

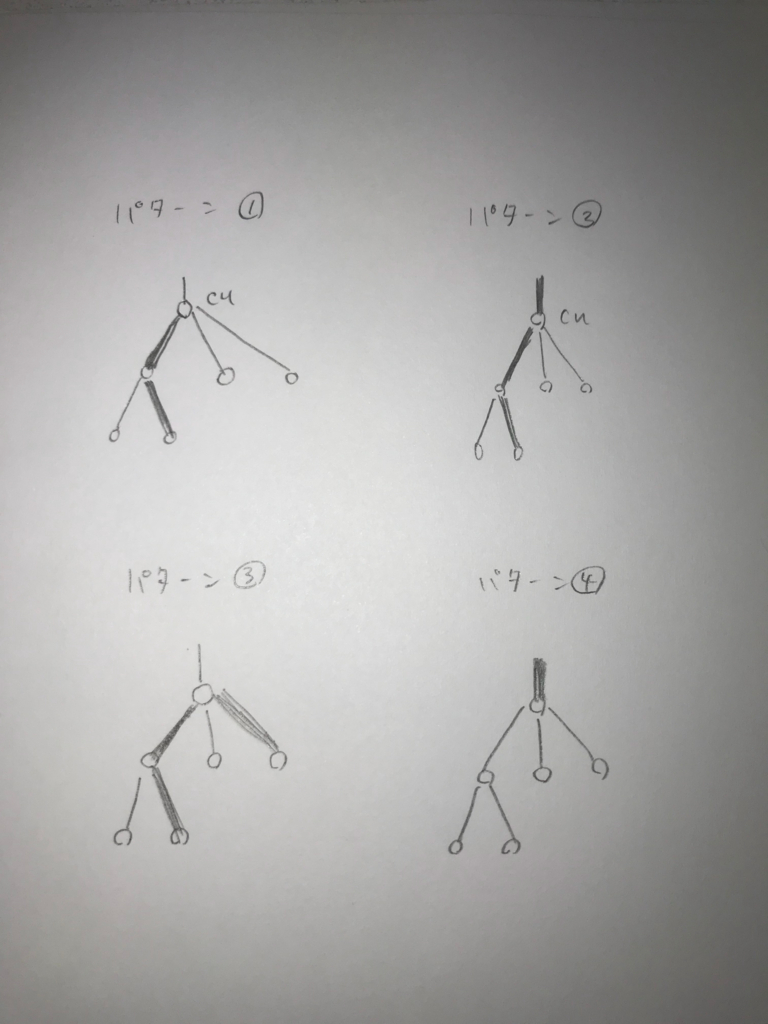
これを達成するために頂点で更にDPをする。
dp2[i][j] := i番目の子まででパスが頂点cuにj個繋がっている時の良い成分の最大個数
これはつなげるならば、dp[child]を足し、繋げないならばK≦cnt[child]のとき良い成分数が1つ増えるという事をやっていく。
あとは、この最終的な結果を使ってパターン1～4を達成する。

int N, K;
vector<int> E[101010];
//---------------------------------------------------------------------------------------------------
int cnt[101010];
void pre(int cu, int pa = -1) {
    cnt[cu] = 1;
    fore(to, E[cu]) if (to != pa) {
        pre(to, cu);
        cnt[cu] += cnt[to];
    }
}
//---------------------------------------------------------------------------------------------------
#define INF INT_MAX/2
int ans = 0;
int dp[101010];
int dp2[101010][3];
void dfs(int cu, int pa = -1) {
    vector<int> children;
    fore(to, E[cu]) if (to != pa) children.push_back(to);
    fore(to, children) dfs(to, cu);
    int M = children.size();
    int up = N - cnt[cu];

    rep(j, 0, 3) dp2[0][j] = -INF;
    dp2[0][0] = 0;

    rep(i, 0, M) {
        int to = children[i];

        if (K <= cnt[to]) {
            rep(j, 0, 3) dp2[i + 1][j] = dp2[i][j] + 1;
        }
        else {
            rep(j, 0, 3) dp2[i + 1][j] = dp2[i][j];
        }

        if (0 <= dp2[i][1]) dp2[i + 1][2] = max(dp2[i + 1][2], dp2[i][1] + dp[to]);
        if (0 <= dp2[i][0]) dp2[i + 1][1] = max(dp2[i + 1][1], dp2[i][0] + dp[to]);
    }
    
    // パターン1
    int an = dp2[M][1];
    if (K <= up) an++;
    ans = max(ans, an);

    // パターン2
    if (M == 0) dp[cu] = 0;
    else dp[cu] = dp2[M][1];

    // パターン3
    an = dp2[M][2];
    if (K <= up) an++;
    ans = max(ans, an);

    // パターン4
    dp[cu] = max(dp[cu], dp2[M][0]);
}
//---------------------------------------------------------------------------------------------------
void _main() {
    cin >> N >> K;
    rep(i, 0, N - 1) {
        int a, b; cin >> a >> b;
        a--; b--;
        E[a].push_back(b);
        E[b].push_back(a);
    }

    pre(0);
    dfs(0);

    cout << ans << endl;
}